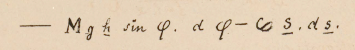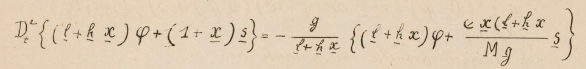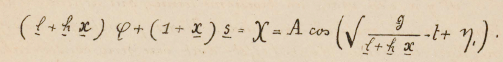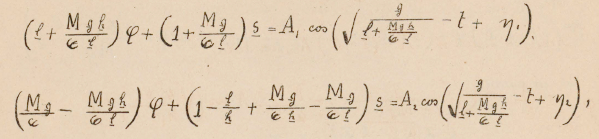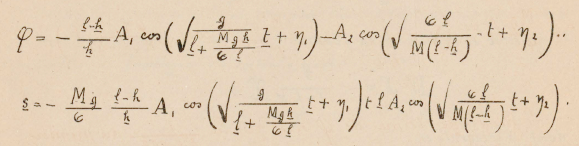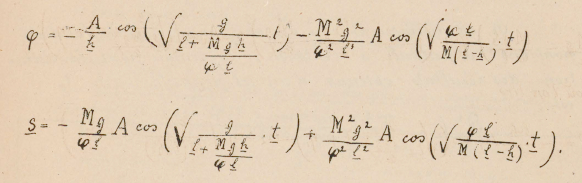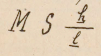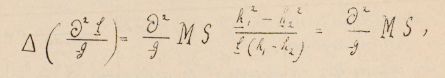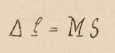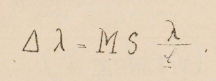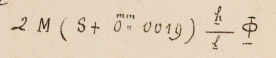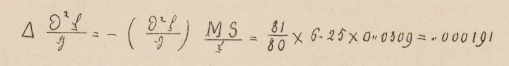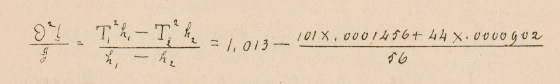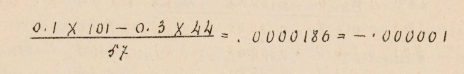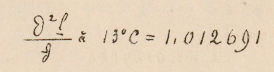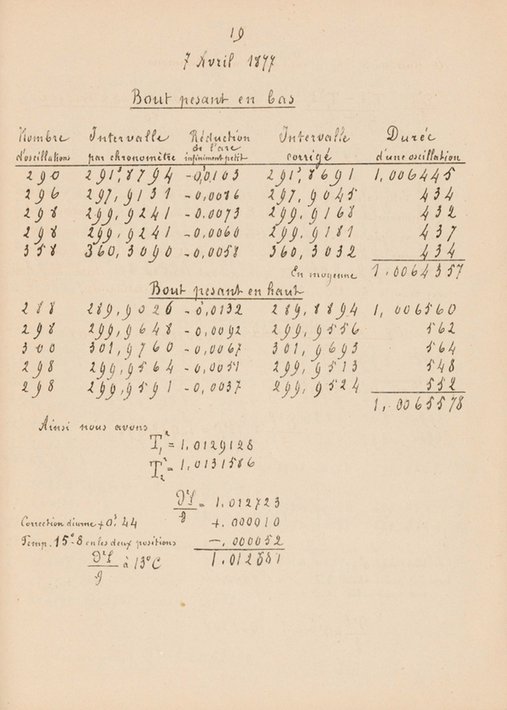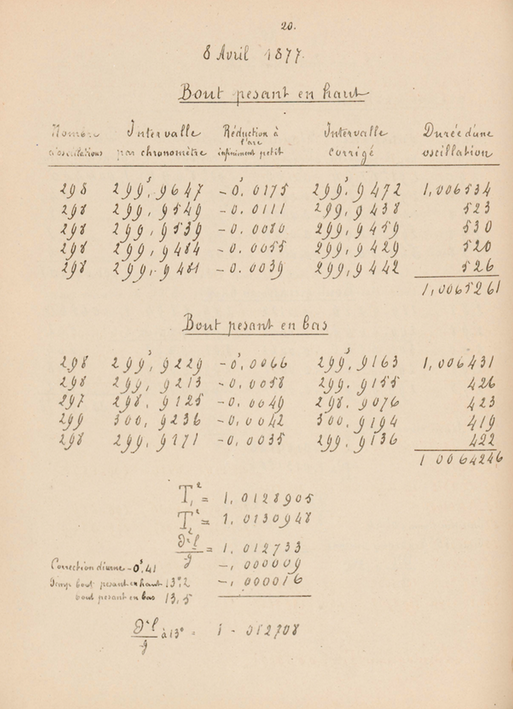
|
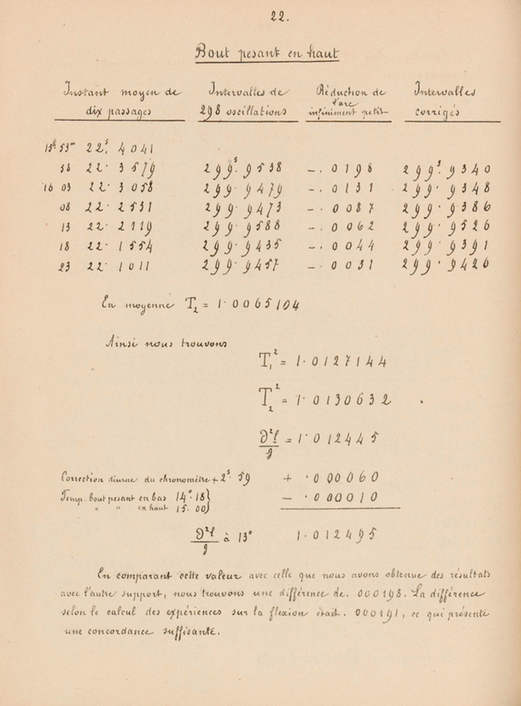
Realizando estas observaciones, percibí claramente la pequeña vibración subsidiaria al final de cada oscilación proveniente del segundo término de la fórmula.
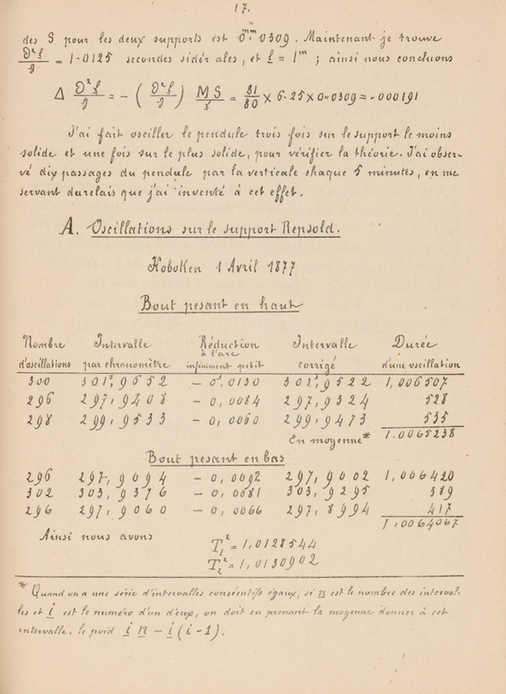
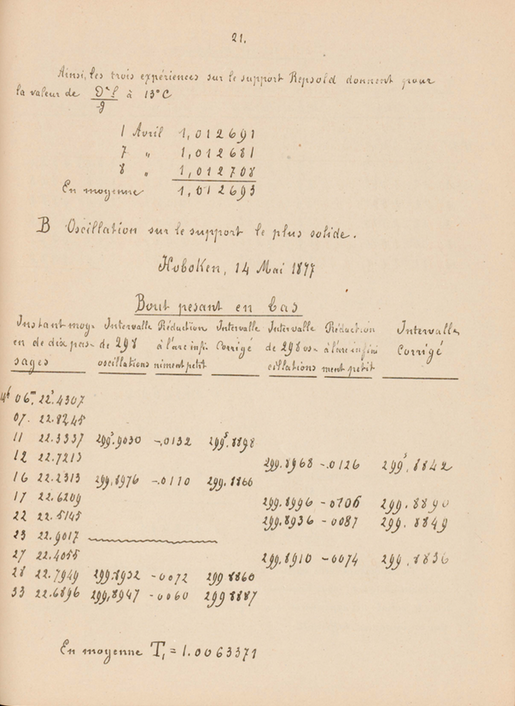
Finalmente hice oscilar el péndulo sobre dos soportes de flexibilidad diferente. El primero de ellos es el soporte Repsold, aquel del que se dan arriba las medidas de flexión. El otro estaba hecho sosteniendo la cabeza del soporte de Repsold en una base gruesa por medio de tuercas de bronce que pasaban por tres agujeros para los tres pies. Estos agujeros son de forma cónica y las tuercas se adaptan perfectamente. He colocado en cada tuerca, entre la cabeza del soporte y la base, una arandela de plomo, de forma que, cortando las tuercas por debajo de la base, la unión resulta más sólida y solucionamos a la vez el nivel, comprimiendo las arandelas. La base, que tiene un grosor de 5 centímetros, ha sido cortada para hacer sitio al péndulo, y ha sido apretada con fuerza entre un muro de piedra y un gran pilar de ladrillos. Ha sido horadada con una pendiente donde podemos hacer entrar la rueda de la máquina Atwood para medir la flexión.
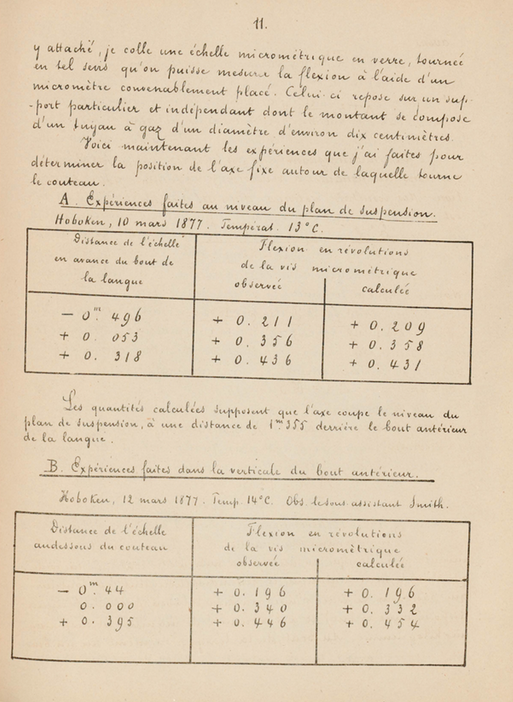
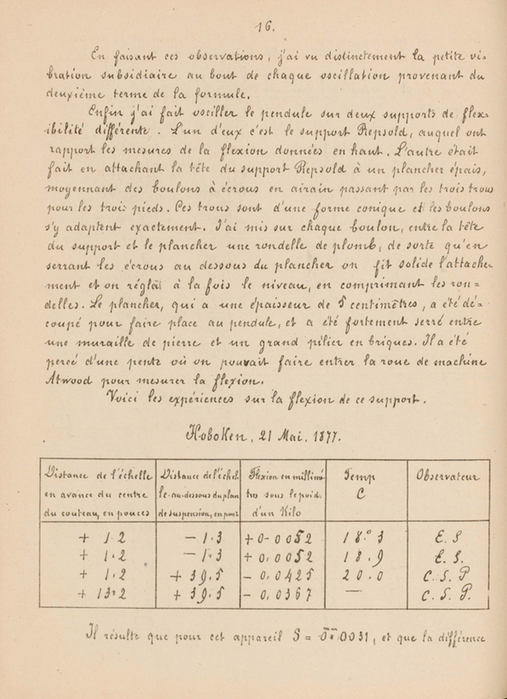
He aquí los experimentos sobre la flexión de este soporte.
Hoboken, 21 de mayo, 1877
| Distancia de la escala por delante del centro del cuchillo, en pulgadas |
Distancia de la escala por debajo del plano de suspensión, en pulgadas |
Flexión en milímetros bajo el peso de un kilo |
Temperatura C |
Observador |
| +1,2 |
-1,3 |
+0,0052 |
18º,3 |
E.S. |
| +1,2 |
-1,3 |
+0,0052 |
18,9 |
E.S. |
| +1,2 |
+39,5 |
-0,0425 |
20.0 |
C.S.P. |
| +13,2 |
+39,5 |
-0,0367 |
—
|
C.S.P. |
Resulta que para este aparejo S=0mm.0031, y que la diferencia
|