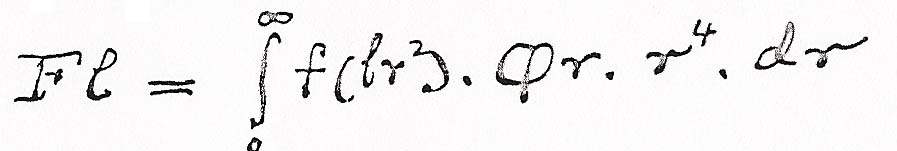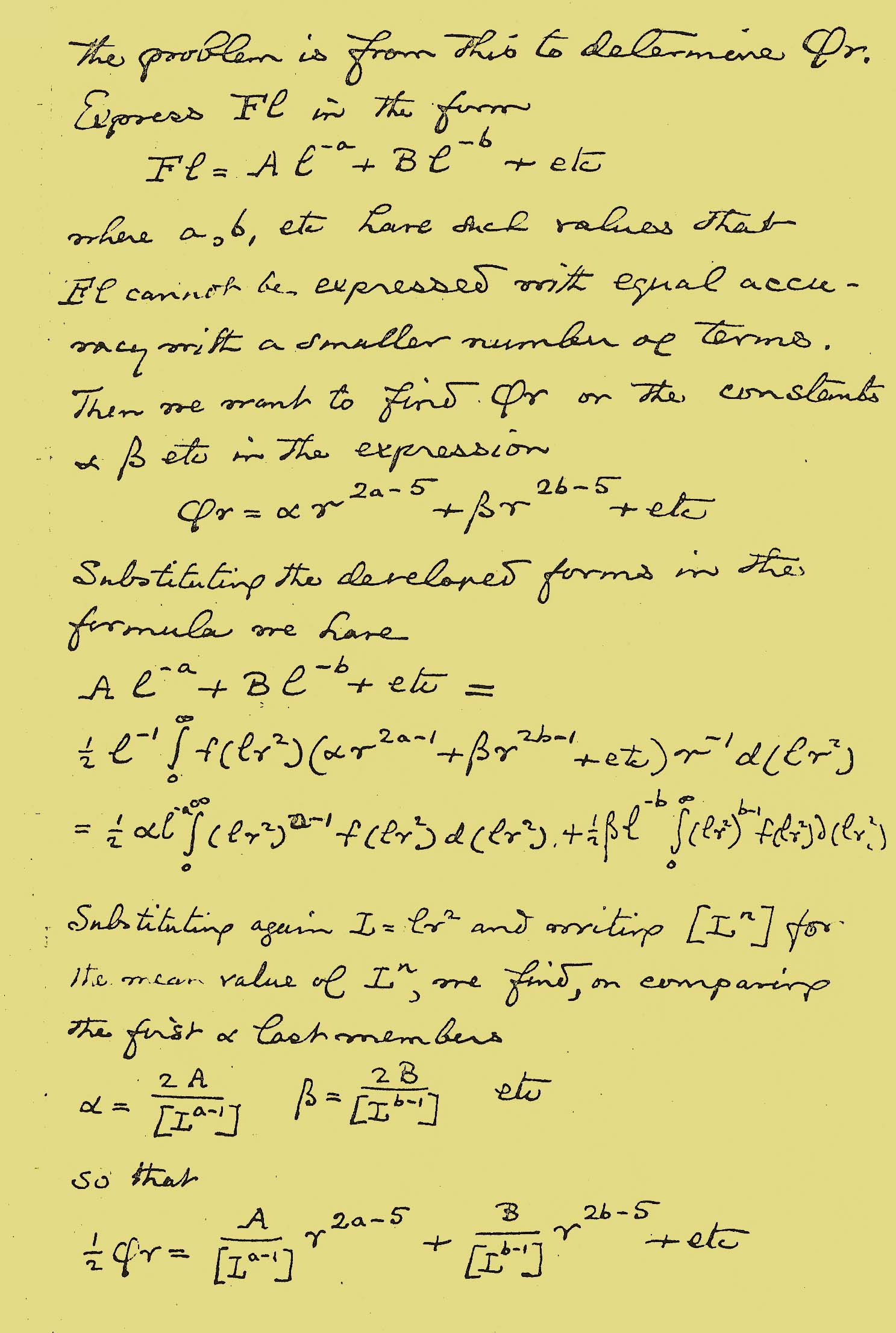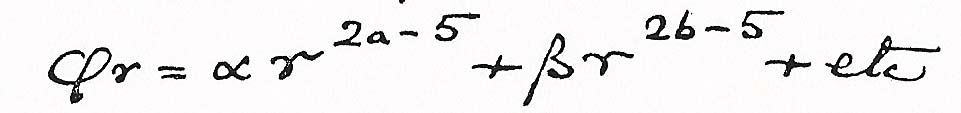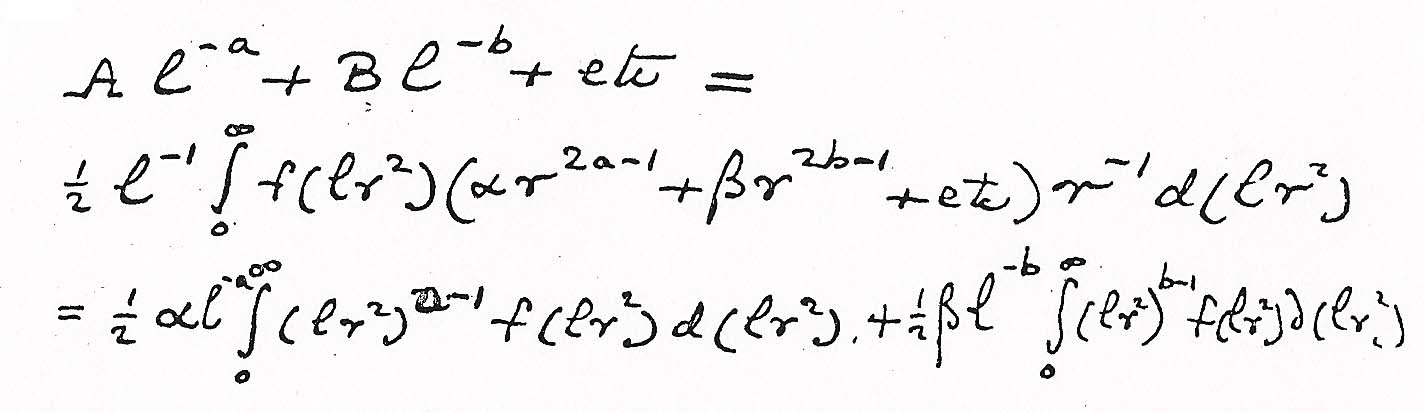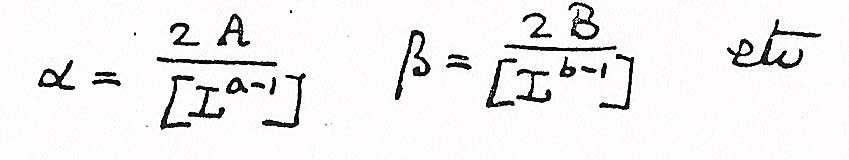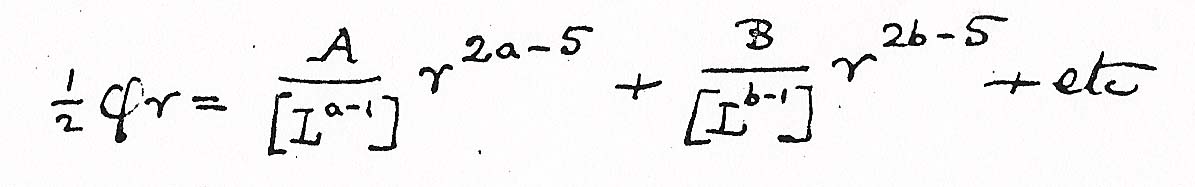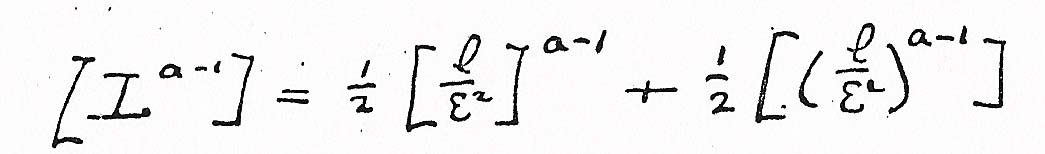Carta de Charles S. Peirce a su madre Sarah Mills
(Ginebra, 07.08.1875)

Esta carta fue escrita por C. S. Peirce a su madre el 7 de agosto de 1875 desde Ginebra, adonde se había trasladado para hacer determinaciones gravimétricas con el péndulo, mientras que Zina se había quedado con su hermana Amy en Berlín.

El original se conserva entre los Charles S. Peirce Papers en la Houghton Library (MS Am 1632, L 341) de la Universidad de Harvard. La reproducción digital de la carta ha sido hecha a partir de la fotocopia disponible en el Peirce Edition Project. Para la transcripción se ha tenido en cuenta la que preparó Max Fisch [VBla(4)#5], accesible también en Indianapolis.

1 Ginebra, 7 de agosto 1875   Mi queridísima madre, He recibido hoy tu carta2 y supongo que debería contestar de inmediato a lo que dices sobre el Observatorio. En primer lugar, no tengo cara para enfrentarme a Newcomb o a Gould, que tienen infinitamente más derecho a ello que yo. Me parece que Gould el que más, aunque Newcomb es por mucho el hombre más fuerte. Gould ha sido suficientemente castigado por su mal temperamento. Además, muchos grandes astrónomos tienen mal genio. El Gran Bairy (Beary)3 y Le Verrier son famosos por eso, y Newton, Flamsteed y un montón de ellos. Quizá trabajar de noche es malo para el humor. Además, no considero que

esa posición sea muy agradable. El lugar tiene muchos aparatos con un personal del todo insuficiente. Así, resulta imposible llegar a hacer alguna investigación allí porque el Director está abrumado por los detalles. Además tienes que vivir en esa casa, que es como un miserable agujero, y en conjunto no es agradable, ni siquiera dejando aparte el hecho espantoso de que tendría que tratar con Eliot4. Por mi parte, espero que Gould lo consiga. Dos hombres tan singularmente desagradables como él y Eliot deberían ser atados juntos por las colas y colgados en un tendedero. Si él lo consigue y ellos pelearan, y si la rueda del tiempo me situara en una posición en la que yo pudiera ayudar a cualquiera de los dos, sería al más débil, para prolongar el com-

bate todo lo que fuera posible. Solo hay dos razones por las que me gustaría ocupar el puesto. Una es que pienso que a Zina podría gustarle5, y la otra es que podría llevar allí los aparatos y los medios para ocuparme de la solución de un problema en el que estoy profundamente interesado, el de la forma del grupo de estrellas en el que estamos, y que incluye a casi todas las estrellas que vemos. Es ciertamente un problema elevado, que apela de forma impresionante a la imaginación, y en diez años o así podría prácticamente resolverlo6. Veo exactamente cómo, y llegaría así a ser toda una figura en la historia de los descubrimientos. Pronto llegarían resultados brillantes, y terminaría el atosigamiento que Winlock sufrió por todas partes y que realmente le mató. Pero no podría

abandonar mi trabajo en el C. S., con el que estoy plenamente comprometido y del que ahora estoy bastante al corriente, y al que estoy dedicándome provechosamente aunque me parece una clase bastante baja de actividad. Mi trabajo fotométrico va a ser impreso en Leipzig por Engelmann, el primer editor científico del mundo7. Va a ser parte de un volumen de los Annals of the H. C. Observatory, del que la otra parte va a imprimirse en casa. Engelmann deseaba comprar 150 copias con autorización para añadir una portada, y añadirlo a la lista de libros publicados por él, un acuerdo altamente favorable para los intereses de los astrónomos, para el observatorio (que vendería así 150 copias de las que ahora no venderá ninguna) y para mí8. Pero Eliot no ha querido. Cualesquiera que hayan sido sus razones han tenido que ser insignificantes. Cuando erija

una sociedad microscópica le haré miembro honorario: una pulga no podría ser más fascinante para un amante de lo infinitamente pequeño. No tienes que enseñarle a papá todo esto acerca de Eliot, ya que él le aprecia y no le gustaría lo que digo. Ciertamente ha hecho bien en tomarse interés por ayudar a la Sra. Winlock9. Siento mucho que no me sea posible sumarme ahora a eso, pero una suma pequeña resultaría peor que ninguna como expresión de mis sentimientos. Sentí y siento muchísimo su muerte, y pasar de pensar en Eliot a pensar en Winlock es de lo más animante posible. No

escribí a ninguno porque el día que me enteré me puse enfermo, en parte por causa de la noticia, pues soy débil y las emociones me afectan físicamente, y tuve que acostarme durante varios días y Zina escribió mientras tanto. Pero el resultado es que mis sentimientos sobre este asunto no han sido expresados; y, si alguna vez estuviera en mi poder hacer tanto por Willie10 como su padre hizo por mí, trataría de imitar la generosa, honesta, caballerosa y gran conducta que convirtió la vida de Winlock en algo satisfactorio incluso para gente no interesada personalmente en ella, igual que las cualidades opuestas en el hombre que tanto le agobió convertirían su muerte en un alivio para todos11. Bien, trataré de dejar esta cuestión.

Aquí viene ahora un trozo para papá. Supongamos que r es la distancia de una estrella L su luz intrínseca efectiva l su luz aparente Entonces (dejando aparte cualquier posible extinción de la luz)                            l= L/r212 Supongamos también que L.dL13 es el número proporcional de estrellas cuya luz está entre L y L+dL; cuya proporción supondré que es la misma en todo el espacio. Sea Φr el número total de estrellas en una unidad de espacio a la distancia r. Sea Fl.dl el número de estrellas cuya luz aparente está entre F14 y l+dl. (Por supuesto Φr y Fl tienen valores diferentes en direcciones diferentes). 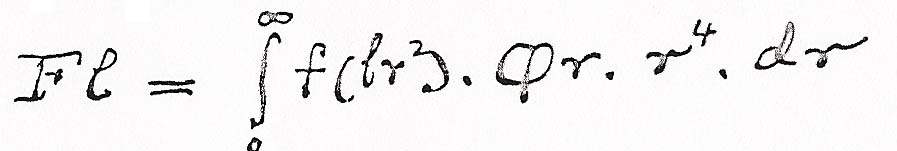Tenemos entonces  La fotometría combinada con la suma de las estrellas nos da Fl en cada parte de los cielos y

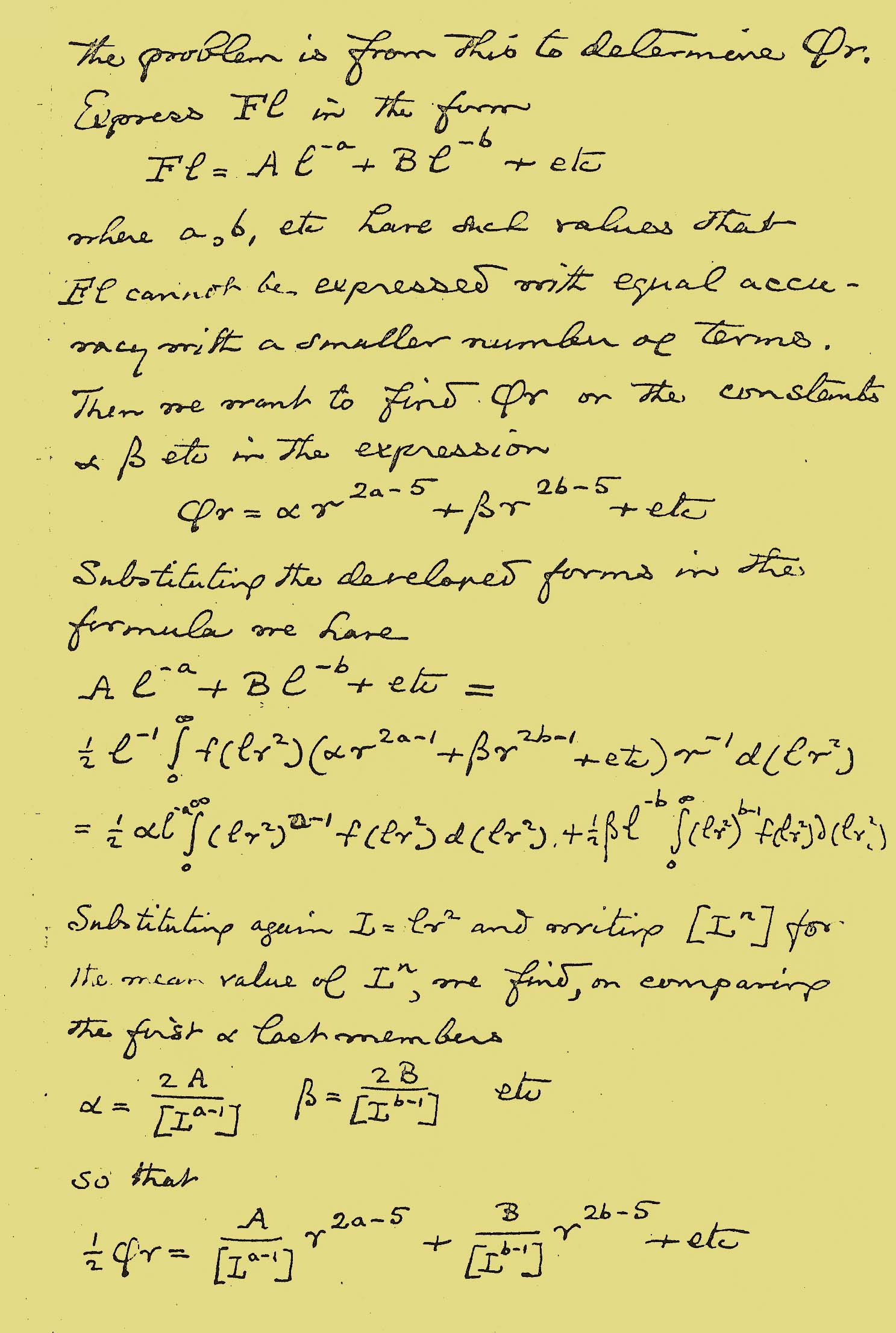
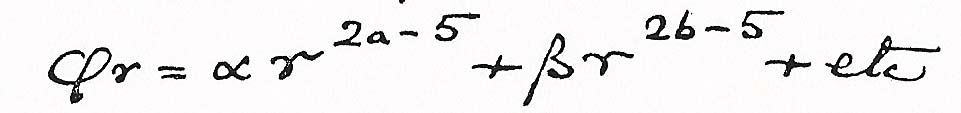
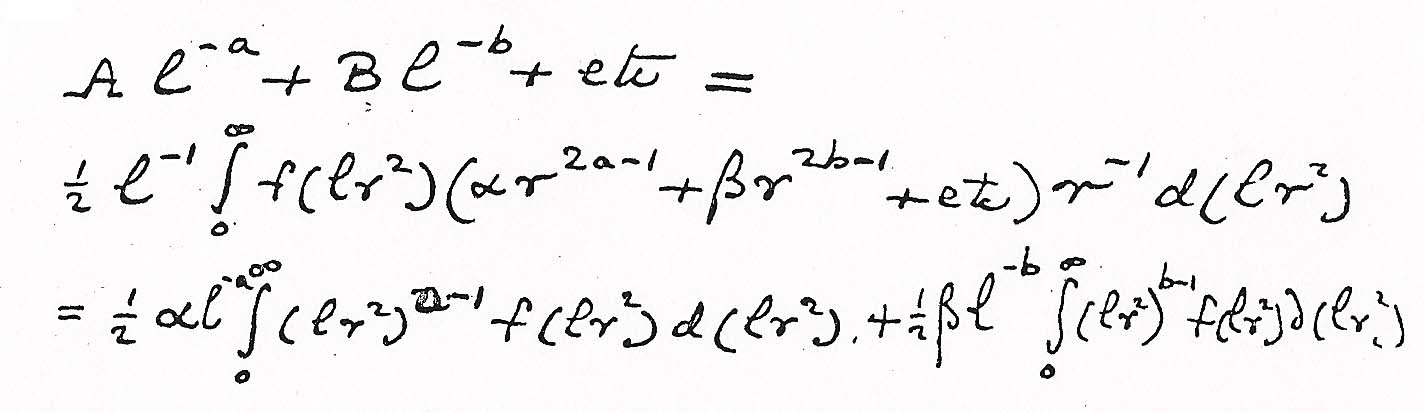
el problema es determinar a partir de esto Φr. Expresemos Fl en la forma Fl=Al-a + Bl-b + etc. Donde a, b, etc. tienen valores tales que Fl no puede expresarse con la misma exactitud con un número más pequeño de términos. Entonces queremos encontrar Φr o las constantes a ß etc. 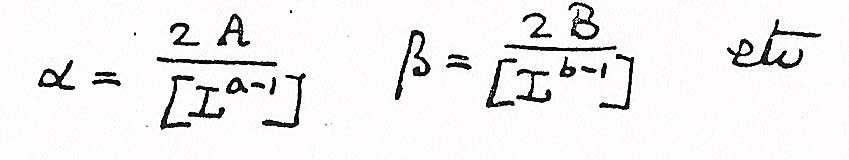en la expresión   Sustituyendo las formas desarrolladas en la fórmula tenemos Sustituyendo de nuevo L=lr2 y escribiendo [Ln] para el valor medio de Ln, encontramos, al comparar el primer y el último miembro de modo que

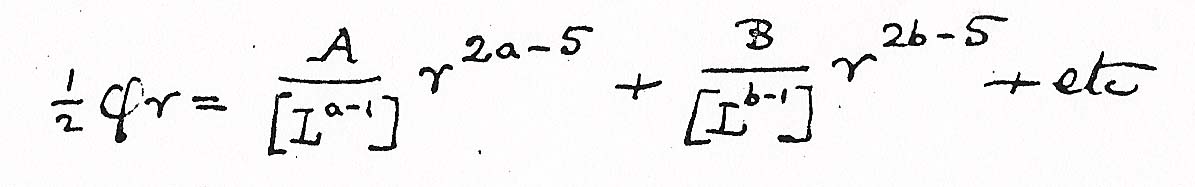
Esto será válido dentro de los límites definidos por r=√l/[L] donde los valores menor y mayor de l han de ser sustituidos15. Ahora bien, para encontrar [La-1] etc. propondría tomar las primeras 200 estrellas más brillantes que sean medidas fotométricamente con exactitud y cuyos movimientos propios, ε, sean también conocidos. Si sus movimientos efectivos en el espacio fueran todos iguales, entonces ε sería inversamente proporcional a r y tendríamos L=l/ε2 y [La-1]=L=[(l/ε2)a-1]. Ya que sus movimientos efectivos en el espacio sin duda varían mucho, los resultados obtenidos para L mediante esta fórmula serían demasiado dispersos. A falta de una investigación sobre la distribución de los movimientos efectivos podemos suponer que esta es similar a (aunque independiente de) la distribución de la luz efectiva que uno puede tomar (si no estoy equivocado)16.

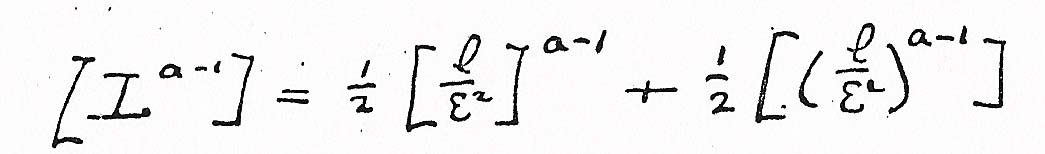
Pienso que de esta manera obtendremos un buen valor suficiente para Φr en toda dirección para encontrar la forma general de las superficies de igual densidad estelar y la posición del sol en el grupo. He dividido los cielos en 32 regiones iguales. Seis en la Vía Láctea, dos zonas de seis cada una a cada lado de la Vía Láctea, y dos regiones en los dos polos de la Vía Láctea. Estoy ahora contando las estrellas en esas regiones descendiendo hasta la 6.3n magnitud. Probablemente no mostrará dónde comienza a descender la densidad en la Vía Láctea, pero mostrará si la Vía Láctea es un anillo y también lo cerca que estamos de uno de sus lados. Si lograra hacer una suma del Durchmusterung descendiendo hasta la magnitud 10n, sería una gran historia. Diez años de observación fotométrica estelar harían todavía más.

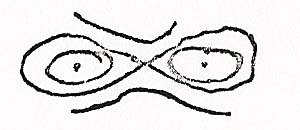
Puedo ver cuáles son los resultados principales aunque todavía no he completado mi trabajo con las estrellas visibles a simple vista. 1. Las superficies internas de igual densidad forman un anillo. 2. Ese anillo es muy irregular pero su sección tiene dos óvalos no muy planos 3. El radio del anillo más denso no está lejos de la distancia de una tercera magnitud estelar. En consecuencia, podemos ver a través de las superficies más densas de la Vía Láctea a simple vista. De hecho, el universo es un pequeño lugar tan miserable que me siento bastante apretado en él desde que averigüé lo pequeño que era. 4. El sol dista del centro de este anillo aproximadamente 1/4 de su radio. 5. El sol está también un poco fuera del plano del anillo en el lado de Coma Berenices.

He ocupado tanto espacio con todo esto que no he dejado nada para las cosas humanas. El hecho es que durante algún tiempo he estado encerrado en mi habitación todo el día trabajando en este asunto. Como consecuencia, no he visto nada. De hecho, desde que Zina me dejó no he visto nada salvo cosas científicas. Estuve en Munich una semana sin entrar a un museo ni ir a ningún sitio excepto a ver a Seidel, Steinheil y Merz17. Me pone enfermo pensar que ella se marcha a casa, pero evidentemente es lo que quiere. No pude convencerla para que viniese a Suiza conmigo. Podría igualmente no tener esposa. No hablo con nadie aquí. En mi desesperación hice que el camarero me sentara ayer en la cena al lado de una mujer inglesa bastante atractiva que había observado que estaba sola, y esas fueron prácticamente las primeras palabras que he dicho. Pero debo animarme y forzarme para ir mañana a Chamonix. Tenía preparado un hermoso viaje, pero Zina no quiso hacerlo. Creo que está disfrutando mucho de la compañía de Tom Burgess18 en Berlín. Pienso a menudo en cuánto me gustaría estar de vuelta en tu casa una vez más. Pienso mucho en todos vosotros, aunque no escriba mucho.

1. En esta carta, como en muchas otras de estos meses, figura impreso lo que parece el escudo de armas de los Peirce. Ver nota 5 de la carta de 2 de mayo de 1875.

2. No se conserva copia de esta carta. Por lo que aquí se dice, Sarah Mills Peirce debió de escribirla poco después del fallecimiento de Joseph Winlock en la mañana del 11 de junio de 1875. Conservamos, en cambio, el telegrama que Benjamin Peirce escribió a Carlile P. Patterson con ese motivo el 11 de junio. Puede leerse el obituario de Winlock, escrito por William A. Rogers.

3. No es clara la lectura de este nombre en la carta. Se refiere probablemente al astrónomo inglés George Biddell Airy (1801-1892), que tenía gran autoridad; quizá a partir de su apellido y de la inicial de Biddell tuviera como apodo "Beary", esto es, osezno.

4. Charles W. Eliot, presidente de Harvard entre 1869 y 1909, conocía bien a Charles S. Peirce pues habían sido compañeros de estudios y se opuso en todo momento a su incorporación a Harvard. Por el contrario, tuvo siempre buena relación con su padre Benjamin Peirce y con su hermano Jem Peirce, que desempeñó cargos directivos en Harvard hasta 1898. Sobre la relación entre Eliot y Charles Peirce puede leerse J. Brent, Charles Sanders Peirce. A Life, 108-111.

5. Este comentario muestra bien que Charles S. Peirce no pensaba que su matrimonio se había roto. De hecho, Zina se reuniría de nuevo con él en el verano de 1876 en Inglaterra, pero se separarán definitivamente al regreso de ambos a Estados Unidos a finales de agosto de 1876. 6. Impresiona que en esta carta a su madre Peirce dé, a pesar de las dificultades obvias que tendría para él asumir el cargo de Director del Observatorio, las razones del gusto de Zina y de su posible dedicación durante diez años al descubrimiento de la forma de la Vía Láctea. A la vez, Peirce es consciente de que no puede abandonar su trabajo en el U. S. Coast Survey aunque le parezca un trabajo común.

Harvard College Observatory, c.1874

7. Wilhelm Engelmann (1808-1878) había aceptado el ofrecimiento de Peirce para hacerse cargo de la edición. En 1878, tres años después, vería la luz el volumen "Photometric Researches by C. S. Peirce. Made in the Years 1872-1875". Sobre el valor de esta obra, puede leerse "Mr. C. S. Peirce's Photometric Researches", Monthly Notices of the Royal Astronomical Society, Vol. 39/4, 1879, 270-273.

8. De hecho, en el espléndido catálogo del centenario de la editorial figura la edición de las Photometric Researches de C. S. Peirce en la página 25 y en la página 259. Se conoce que, después de las negociaciones, autorizaron a Engelmann esa edición aparte de 150 ejemplares.

9. Se trata de Mary Isabella Lane (1832-1912), que se había casado con Joseph Winlock en Shelbyville, Kentucky, el 10 de diciembre de 1856. A la muerte de su marido, tenían seis hijos. La mayor, Anna Winlock (1857-1904), será astrónoma en Harvard, como también William Crawford Winlock (1859-1896).

10. William C. Winlock (1859-1896) trabajó en el U.S. Coast Survey colaborando con Charles S. Peirce en 1874 en la determinación de la fuerza de gravedad en el Hoosac Tunnel. Se graduó en Harvard en 1880 y colaboró como ayudante en el Observatorio de Harvard. Fue el autor de "Observations of the Great Comet of 1882" (Washington, 1883) y de "Bibliography of Astronomy for the Year 1887" (Washington, 1888). Puede leerse su perfil biográfico, escrito por S. P. Langley (1834-1906).

11. La lectura de este pasaje es quizá dudosa pero puede ser interpretada como que Charles S. Peirce está diciendo que Winlock había fallecido por el agobio al que el Presidente Eliot le sometió, y que sería un alivio para todos la desaparición de Eliot.

12. Esta fórmula expresa que la luz aparente que recibimos de una estrella va disminuyendo en función de la distancia a la que nos encontramos. Decae como el cuadrado de la distancia porque la luz que emite la estrella se distribuye de manera homogénea en todas direcciones, así que la parte que llega a nosotros va disminuyendo de manera inversamente proporcional al área de la superficie de una esfera imaginaria en la que nos encontraríamos, cuyo radio sería la distancia a la estrella.

13. Quizá aquí Peirce debería decir fL.dL. fL, o mejor f(L), pues es la densidad de probabilidad de que una estrella tenga luminosidad entre L y L+dL.

14. Quizá debería ser "l", no "F".

15. Simplemente está señalando los límites de aplicación de las expresiones teniendo en cuenta los datos experimentales de que se disponga. No tendría sentido extrapolarlos a regiones del espacio que no caen dentro del rango cubierto por los valores de luminosidad aparente que se obtienen.

16. Dicho de otra manera, Peirce supone que la cantidad de luz intrínseca de las estrellas es prácticamente constante, y que las variaciones en la luz aparente provienen fundamentalmente de sus movimientos propios (que cambian su distancia a tierra y, por tanto, la luz aparente que nos llega de ellas). Actualmente se considera la densidad estelar en función únicamente de la distribución de luz aparente que se mide en cada dirección del espacio.

Parece que la siguiente fórmula es una simplificación que introduce Peirce para evitar una gran dispersión en los momentos altos de la distribución a partir de las medidas experimentales de que se dispone. Desconocemos por el momento en qué se fundamenta para hacerlo así.

17. Se trata de los conocidos fabricantes de instrumentos científicos en Múnich.

18. Thomas Burgess (1842-1912), graduado en 1861 en la Universidad de Harvard y en 1864 en la Universidad de Oxford. Puede leerse en las páginas 22 y 23 del Secretary's Report, Harvard College, Class of 1860, un perfil biográfico de Burgess. Era hermano de Edward Burgess con quien Benjamin Peirce mantuvo correspondencia.

Traducción de Sara Barrena (2013)

Una de las ventajas de los textos en formato electrónico respecto de los textos impresos es que pueden corregirse con gran facilidad mediante la colaboración activa de los lectores que adviertan erratas, errores o simplemente mejores traducciones. En este sentido agradeceríamos que se enviaran todas las sugerencias y correcciones a sbarrena@unav.es

Proyecto de investigación "Charles S. Peirce en Europa (1875-76): comunidad científica y correspondencia" (MCI: FFI2011-24340)

Fecha del documento: 12 de febrero 2013
Última actualización: 10 de agosto 2021