Carta de Charles S. Peirce a W. S. Jevons
(Pest, 25.08.1870)
Esta carta,
fechada el 25 de agosto de 1870, fue escrita por C. S. Peirce desde Pest al
lógico y economista británico Stanley Jevons (1835-1882). Jevons
fue uno de los primeros en tratar de introducir el rigor matemático en
la economía. En esta carta, respuesta a
una de Jevons no localizada, Peirce discute con él algunos detalles de
su concepción de las operaciones matemáticas y de la idea del
razonamiento como sustitución.
El original se conserva en la Manchester University Library. La reproducción
digital de la carta ha sido hecha a partir de la fotocopia disponible en el
Peirce Edition Project. Para la transcripción de la carta se ha tenido
en cuenta la que preparó Max Fisch, accesible también en Indianapolis.
La carta fue también publicada en W2, pp. 445-6.
|
Pest.
25 de agosto 1870
Estimado Señor
Recibí hace
unos días su gratificante carta1 desde Inglaterra y, como me parece
que usted es el único que trabaja activamente sobre lógica
matemática, deseo mucho exponer mis opiniones ante usted con
sus verdaderos colores, y responderé por tanto a dos de los puntos
contenidos en su carta.
Parece que usted
no acepta mis definiciones ampliadas de las operaciones matemáticas.
Serán los matemáticos quienes decidan la validez de esa
generalización, y pienso que aceptarán mis definiciones.
Respecto a la adición y la multiplicación, en efecto,
la única novedad en mi postura es que no considero como esencial
a estas operaciones que sean "invertibles". Ahora bien,
me parece que el estudio del cálculo de funciones no nos lleva
a considerar esta característica como muy significativa, sino
que, por el contrario, el que una operación sea invertible se debe
usualmente a una restricción de su aplicación. Así,
cuando no tomamos en consideración las cantidades negativas |
|
e imaginarias la
involución es invertible. Si la adición se considera como
esencialmente invertible, entonces la operación es aplicable
a algunos términos lógicos y a otros no. Ahora bien, entendería
muy mal el espíritu del álgebra moderna si no fuera contrario
a él no ampliar la definición de adición bajo esas
circunstancias. Obsérvese que no puede dejarse completamente
fuera de la lógica a la adición, pues en el momento en
que se toma = como signo de identidad, esto es, que se concibe la igualdad
como un caso de la identidad, la adición se hace por ello aplicable
a términos mutuamente exclusivos.
Por supuesto la
adición no es esencialmente invertible ni tampoco lo es la multiplicación.
No acabo de ver cómo usted puede decir que uso el término
multiplicación de una manera del todo desconectada de su significado
original. Tomemos la definición de la página 3 de mi artículo.
No difiere en ningún aspecto de las concepciones ahora universalmente
admitidas, excepto en relación al carácter "invertible".
Pero tomemos mi multiplicación lógica habitual. Pienso
que he mostrado en la p. 15 que la concepción de la multiplicación
entre cuaterniones es exactamente la misma que la mía y que la
multiplicación numérica
|
|
es
meramente un caso de mi operación.
Me parece que usted sostiene que todo razonamiento se da mediante
sustituciones (en lo que coincido con usted); que todas las sustituciones,
cuando son algebraicamente denotadas, aparecen como la sustitución
de iguales por iguales, que, por tanto, la cópula significa igualdad
y que la teoría del predicado cuantificado se sostiene. Pero
me figuro que la segunda premisa sería difícil de justificar.
Observará que en una nota de la p. 2 he mostrado rígidamente
que de acuerdo a principios admitidos la concepción de = está
compuesta de las concepciones de  y y (o
(o 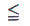 y y 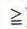 ).
Siendo esto así el silogismo-sustitución: ).
Siendo esto así el silogismo-sustitución:
A=B B=C
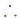 A=C A=C
es un compuesto de los dos
y al analizar inferencias el lógico debería representarlo
así. ¿Qué respuesta hay a mi nota o a la conclusión
que extraigo de ella? En la práctica es mucho más fácil
manipular el cálculo lógico con como
cópula que con =. como
cópula que con =.
Dudo especialmente
de la posibilidad de un tratamiento exitoso de las sustituciones del
razonamiento científico basado en los principios de la teoría
del
|
|
predicado
cuantificado. En un artículo anterior2 traté de mostrar que
toda inferencia procede mediante la sustitución de un signo por
otro según el principio de que el signo de un signo es un signo,
que el razonamiento se diferencia de acuerdo con las diferentes clases
de signos con las que trata, y que los signos son de tres clases, primero,
cosas similares a sus objetos, segundo, cosas físicamente conectadas
con sus objetos, como el ruborizarse es un signo de vergüenza, tercero,
signos generales3. La sustitución de un signo general da el razonamiento
deductivo; la sustitución de similares da el razonamiento hacia
una hipótesis, como cuando digo por ejemplo que el abrigo, el sombrero,
el modo de hablar, etc. de este hombre son como los de un cuáquero
y por tanto supongo que lo es; la sustitución de signos físicos
da la inducción, como cuando digo por ejemplo que todas estas muestras
han sido extraídas al azar de esta colección y por lo tanto
la manera en la que han sido físicamente extraídas hace
necesario que sean un signo de aquello en lo que consiste la colección.
Ya que por tanto estas son bolas rojas toda la colección es de
bolas rojas.
Confío en que
esta discusión le interesará lo suficiente como para continuarla
y quedo con gran respeto Sinceramente suyo.
C. S. Peirce
Las cartas dirigidas
a Robt. Thode & Co.4 Berlín
me llegarán. |
Notas
1.
No se ha
localizado esa carta que Jevons
debió de enviar a Peirce comentando algunas cuestiones relativas al trabajo
"Description of a Notation for the Logic of Relatives, Resulting from an
Amplification of the Conceptions of Boole's Calculus of Logic" (W2: 350-429). Muy probablemente
Peirce no llegó a encontrarse personalmente con Jevons en Londres en
el mes de julio, pues Jevons estaba de vacaciones en su casa de Manchester y
en la costa (Cf. Letters and Journal of W. Stanley Jevons (1886), London,
Macmillan, p. 251).
Se trataba de la memoria
que Peirce había leído ante la American Academy of Arts and
Sciences el 26 de enero precedente. "Es una de las obras más
importantes en la historia de la lógica moderna, pues es el primer intento
de expandir el álgebra lógica de Boole para incluir la lógica
de relaciones" ha escrito Daniel D. Merrill, "The
1870 Logic of Relatives Memoir" (W2.xliii-xlviii)".
2.
Quizá se refiere a "Algunas
consecuencias de cuatro incapacidades" (1868) donde da cuenta del papel
de la sustitución en el silogismo (n. 16): "Cada uno de los términos
de tal proposición está o en lugar de ciertos objetos o de ciertas
características. La conclusión puede considerarse como una proposición
que viene a sustituir a cada una de las premisas, justificándose tal
sustitución por el hecho enunciado en la otra premisa. Consiguientemente,
la conclusión se deriva de cada una de las dos premisas, sustituyendo
o un nuevo sujeto por el sujeto de la premisa, o un nuevo predicado por el predicado
de la premisa, o por ambas sustituciones. Ahora bien, las sustituciones de un
término por otro se justifican sólo en la medida en que el término
sustituido representa sólo lo representado en el término reemplazado".
3.
Se trata de una de las primeras formulaciones de la conocida clasificación
peirceana de los signos entre "icono", "índice" y
"símbolo". Para más información puede verse la
colección de textos "El
icono, el índice y el símbolo" (c.1893-1903) y "¿Qué
es un signo?" (1894).
4.
Se trata de una entidad
bancaria, fundada en 1832, que sería adquirida en 1892 por el Dresdner
Bank.
Traducción
de Sara Barrena (2008)
Una de
las ventajas de los textos en formato electrónico respecto de los textos
impresos es que pueden corregirse con gran facilidad mediante la colaboración
activa de los lectores que adviertan erratas, errores o simplemente mejores
traducciones. En este sentido agradeceríamos que se enviaran todas las
sugerencias y correcciones a sbarrena@unav.es
Proyecto
de investigación "La correspondencia europea de C. S. Peirce: creatividad y
cooperación científica (Universidad de Navarra 2007-09)
Fecha del documento: 27 de mayo 2008
Última actualización: 9 de agosto 2021
[Página
Principal]





