"A Theory of Probable Inference. Note B. The Logic of Relatives" se publicó originalmente en Studies in Logic by members of the Johns Hopkins University, Boston, 1883, pp. 187-203 y fue recogido en CP 3.328-358. La traducción castellana de Pilar Castrillo se publicó en Charles S. Peirce. Escritos lógicos, Alianza Editorial, Madrid, 1988.
Un término relatico diádico como, por ejemplo, "amante", "benefactor", "sirviente", es un nombre común que designa un par de objetos. De los dos miembros del par, el determinante es generalmente el primero, y el determinado el segundo, de suerte que si se cambia el orden, el par no se considerará ya el mismo.
Sean A, B, C, D, etc., todos los objetos individuales del universo; entonces todos los pares individuales pueden disponerse en un cuadro del siguiente modo:
Un relativo general puede considerarse como un agregado lógico de algunos de tales relativos individuales. Supongamos que l denota "amante", entonces podemos escribir
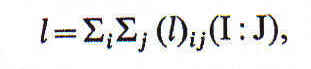
en donde (l)ij es un coeficiente numérico, cuyo valor es 1 en el caso de que I sea un amante de J y 0 en el caso contrario, y en donde las sumas han de tomarse por todos los individuos del universo.
Todo término relativo tiene una negación (lo mismo que cualquier otro término)
que puede representarse trazando una línea recta sobre el signo del propio relativo.
La negación de un relativo incluye todo par excluido por éste y viceversa. Todo
relativo tiene también un converso, que se obtiene cambiando el orden
los miembros del par. Así, el converso de "amante" es "amado".
Este converso puede representarse trazando una línea curva sobre el signo del
relativo, así: 
Se define por
la ecuación siguiente:
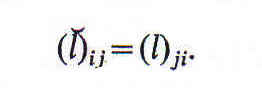
Las siguientes fórmulas, aunque obvias, son importantes:
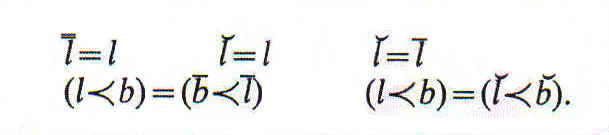
Los términos relativos pueden agregarse y componerse como los demás. Empleando + como signo de agregación lógica y la coma como signo de composición lógica (la multiplicación booleana, que aquí ha de llamarse multiplicación interna o no-relativa), tenemos las definiciones
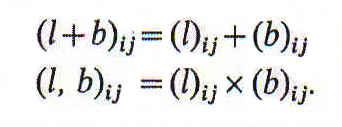
Sin embargo, la primera de esas ecuaciones ha de entenderse de un modo peculiar, por cuanto que el signo + del segundo miembro no es una adición en sentido estricto, sino una operación por la que
0+0= 0 0+1= 1+0=1+1= 1
En lugar de (l)ij+(b)ij, se podría escribir con más exactitud
00(l)ij+(b)ij.
Las principales fórmulas de agregación y composición son:
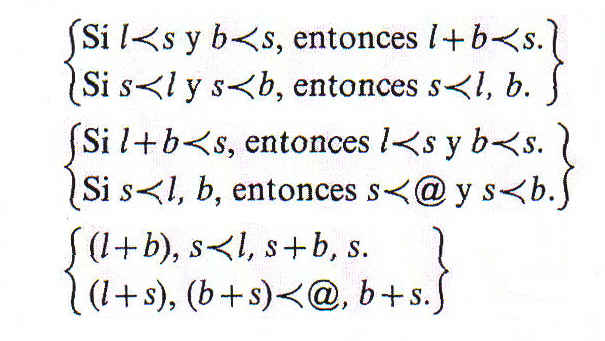
En cuanto a las fórmulas subsidiarias, como son las mismas que las de la lógica no relativa, no es preciso que las expongamos.
Llegamos ahora a la combinación de relativos. Representamos dos de tales operaciones mediante símbolos específicos; a saber, escribimos
lb para amante de un benefactor
y
l † b para amante de todo menos de los benefactores.
La primera se dice que es una combinación particular porque implica la existencia
de algo amado por su relato y un benefactor de su correlato.
En cambio, la segunda se dice que es universal, ya que implica la no-existencia
de cosa alguna, salvo de lo que o bien es amado por su relato o bien es
un benefactor de su correlato. La combinación lb se denomina producto
relativo, la l † b la suma relativa. De l y de b
se dice que no están distribuidos en ninguna de ambas, ya que si 
,
entonces 
y 
;
y si 
, entonces 
y
Ambas combinaciones se definen mediante las ecuaciones
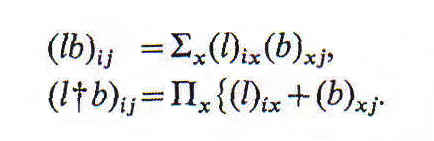
El signo de adición de la última fórmula tiene el mismo sentido que en la ecuación que define la multiplicación no-relativa.
La adición y la multiplicación relativas están sujetas a la ley asociativa. Esto es:
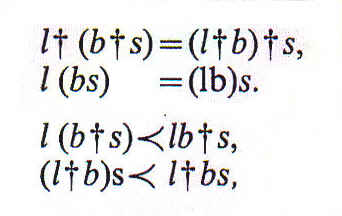
son dos fórmulas tan frecuentemente empleadas que difícilmente puede hacerse nada sin ellas.
La primera afirma que todo lo que es amante de un objeto que es benefactor de todo menos de un sirviente está con todo lo que no sean sirvientes en la relación de amante de un benefactor. La segunda afirma que todo lo que está con un sirviente en la relación de amante de todo lo que no sean sus benefactores es un amante de todo menos de los benefactores de los sirvientes. Las siguientes fórmulas son obvias y triviales:
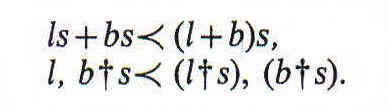
En cambio, no son obvias, aunque sí importantes, estas otras:
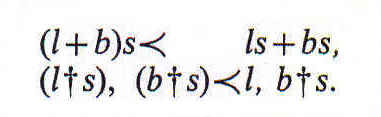
Hay algunas fórmulas de desarrollo curiosas. Tal es el caso de
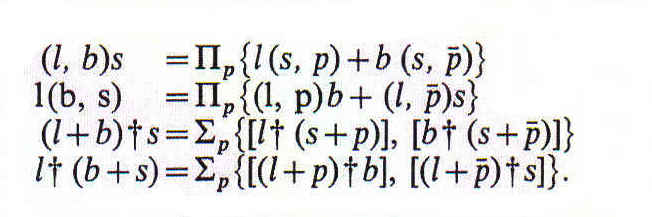
Las sumas y multiplicaciones denotadas por ∑ y ∏ han de ser tomadas en sentido no relativo y todos los términos relativos han de ser sustituidos sucesivamente por p.
Las negaciones de las combinaciones siguen las siguientes reglas:
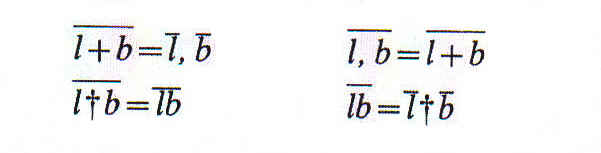
Las conversas de las combinaciones son las siguientes:
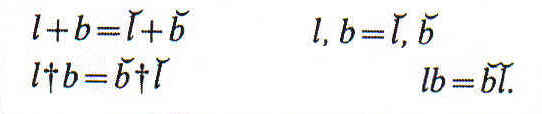
Los relativos diádicos individuales son de dos tipos:
A : A y A : B
Los relativos que no contienen ningún apareamiento de un objeto consigo mismo se llaman alio-relativos por contraposición a los auto-relativos. Las negaciones de alio-relativos aparean todo objeto consigo mismo. Los relativos que no contienen ningún apareamiento de un objeto con otra cosa que él mismo se llaman concurrentes por contraposición a los oponentes. Las negaciones de concurrentes aparean todo objeto con cualquier otro.
No hay más que un solo relativo que aparee cualquier objeto consigo mismo y con todos los demás. Es el agregado de todos los pares y se representa mediante ∞. Se lo traduce al lenguaje ordinario mediante la expresión "coexistente con". Su negación es 0. No hay más que un solo relativo que aparee todo objeto consigo mismo y con ninguna otra cosa. Es
(A : A) + (B : B) + (C : C) + etc.;
se representa mediante 1 y en el lenguaje ordinario se lo traduce por "es idéntico con — —»». Su negación representada mediante л es "otro que" o "no".
Cualquiera que sea el término relativo x, tenemos
Por consiguiente, es evidente que
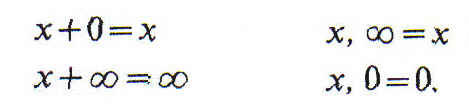
Las últimas fórmulas valen para las operaciones relativas; por tanto,
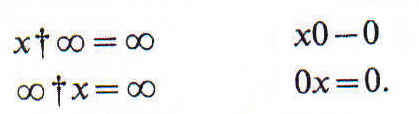
Las fórmulas
también valen si sustituimos ∞ por las operaciones relativas y también por 1 y 0 por л; por tanto tenemos
También tenemos
a las que corresponde en parte el siguiente par de importantísimas fórmulas:
La lógica de relativos es enormemente multiforme; se caracteriza por sus innumerables inferencias inmediatas y por las diversas conclusiones distintas susceptibles de ser derivadas de los mismos conjuntos de premisas. Un ejemplo es la primera de estas características nos los ofrece Mitchell con su F1v siguiéndose de F1v'. Como por ejemplo de la segunda, consideremos las premisas:
Todo hombre es amante de un animal
y
Toda mujer es amante de un no-animal.
A partir de ellas podemos inferir igualmente que
Todo hombres es amante de algo que está con cada mujer en la relación de no ser la única cosa amada por ella, y que
Toda mujer es amante de algo que está con cada hombre en la relación de no ser la única cosa amada por él.
Toda mujer es amante de algo que está con cada hombre en la relación de no ser la única cosa amada por él.
La consecuencia que se sigue de estas peculiaridades es que esta álgebra no puede estar sujeta a reglas tan sólidas y firmes como las del cálculo booleano y quetodo lo que se puede hacer aquí es dar una idea general de la forma en que se puede operar con ella. El estudiante debe empezar por desconfiar de la idea de que los instrumentos clave del álgebra son las operaciones inversas. El álgebra general apenas conoce operación inversa alguna. Cuando una operación inversa se identifica con una directa con una cantidad inversa (como se identifica la sustracción con la adición de la negación y la división con la multiplicación por la recíproca) puede ser un instrumento útil; de lo contrario es casi siempre inútil. En el álgebra ordinaria hablamos del "valor principal" del logaritmo, etc., que no es sino una operación directa resultado de sustituir una operación inversa indefinidamente ambigua. Sin embargo, la eliminación y transposición dependen en realidad en este álgebra de fórmulas completamente análogas a las fórmulas
del álgebra aritmética. Tales fórmulas son
Por ejemplo, para eliminar s de las proposiciones.
multiplicamos una por otra en tal orden que queden juntas las s's de ambas y luego aplicamos la segunda de las fórmulas anteriores, del siguiente modo:
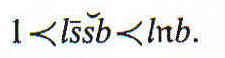
Este ejemplo muestra la utilidad de las fórmulas asociativas para juntar letras. Otras fórmulas que también tienen gran interés desde este punto de vista son las siguientes:
Las fórmulas distributivas también son útiles para este propósito.
Una vez que la letra que había de eliminarse ha sido reemplazada por alguno de los cuatro relativos —0, ∞, l, л— generalmente, el relativo que la reemplaza puede ser eliminado mediante alguna de las fórmulas siguientes:
Cuando sólo tengamos que habérnoslas con proposiciones universales, convendrá
traspasar todo del sujeto al predicado con objeto de convertir al sujeto en
l. Así, si lo que se nos da es 
podemos
añadir 
en ambos lados, con
lo que tendremos
Toda proposición estará por tanto en una de las dos formas siguientes:
En una proposición de la forma 
es correcto (1) transponer los términos y (2) sustituirlos por sus conversas.
Así, las siguientes proposiciones son equivalentes:
En una proposición de la forma 
lo único que podemos hacer es sustituir el predicado por su conversa resultado
Con tres términos hay cuatro tipos de proposiciones universales, a saber:
De estas cuatro formas, la tercera es una inferencia inmediata de la segunda.
A modo de ilustración, podemos resolver los silogismos cuyas premisas son las proposiciones de primer orden mencionadas en la Nota A. Sean a y c términos de clase, y sea β un grupo de propiedades. Sea p el relativo "poseer como propiedad". Los términos no-relativos han de ser considerados como relativos —interpretando, por ejemplo, a como "coexistente con" y ă como "coexistente como un a que es". Entonces las seis formas de proposiciones afirmativas de primer orden son
Los diferentes tipos de silogismo son los siguientes:
Sustituyamos por su conversa una de las premisas y multipliquemos,
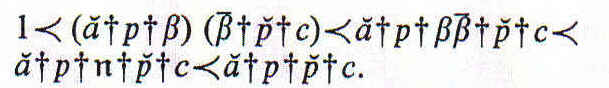
El tratamiento sería el mismo caso de que una o las dos premisas fueron negativas, esto es, contuvieran ¯p en lugar de p.
Tenemos
y lo mismo ocurre con las negaciones.
y lo mismo ocurre con las negaciones
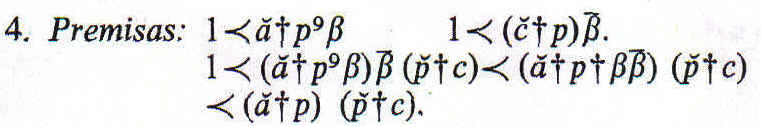
Si una de las premisas, por ejemplo la primera, fuera negativa, obtendríamos una conclusión similar:
pero de ella se podría a su vez eliminar p, resultando
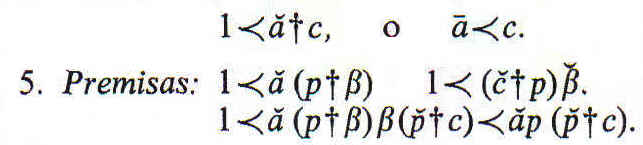
Si alguna de las dos premisas fuera negativa podría eliminarse p,
resultando 
o algún a
es c.
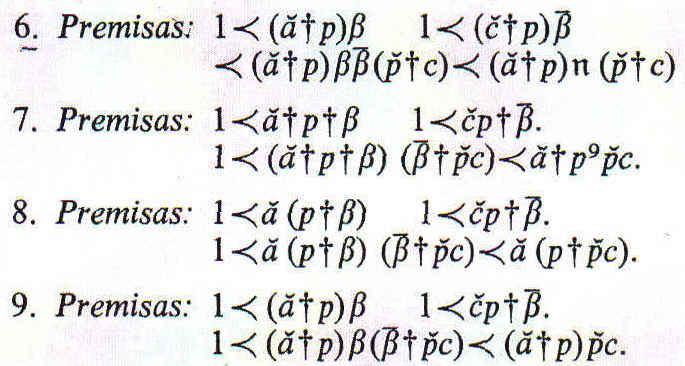
Si una premisa es negativa, tenemos la conclusión última
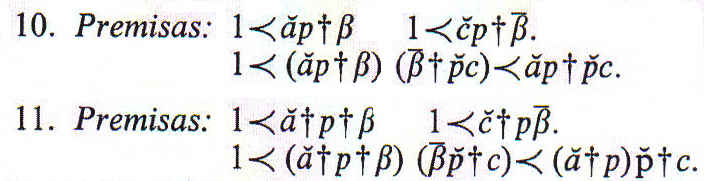
También podríamos concluir
pero esta conclusión es una inferencia inmediata de la otra; dado que
Si una de las premisas es negativa, tenemos como conclusión final 
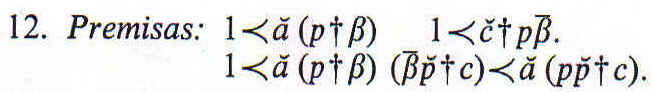
Si una de las premisas es negativa, tenemos como inferencia final
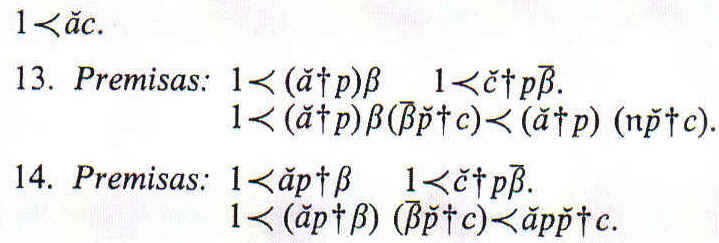
Si una de las premisas es negativa, tenemos la falsa inferencia 
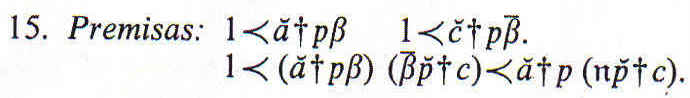
También podemos inferir
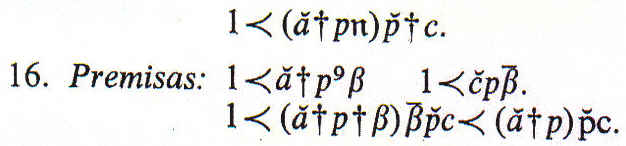
Si una de las premisas es negativa, podemos inferir finalmente 
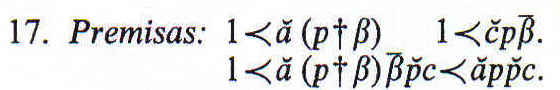
Si una de las premisas es negativa, tenemos la falsa conclusión final 
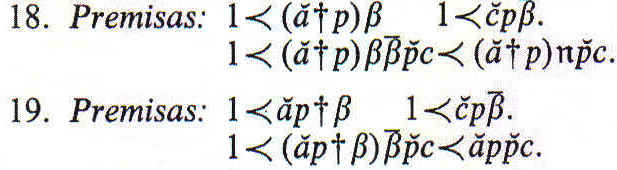
Si una de las premisas en negativa, concluimos finalmente
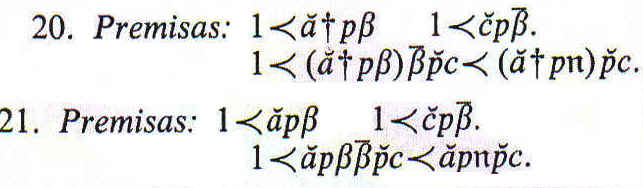
Cuando tenemos que tratar con proposiciones particulares, tenemos la proposición
, o lo que es lo mismo, "algo
existe", pues toda proposición particular implica esto. Entonces toda proposición
particular puede expresarse en alguna de las cuatro formas siguientes:
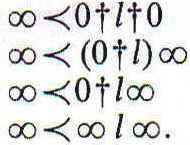
Cada una de estas proposiciones se sigue inmediatamente de alguna anterior.
Las expresiones involucradas que forman los predicados tienen la singular
propiedad de que cada una es o bien 0 o bien ∞. Este hecho
confiere una libertad extraordinaria a la hora de usar las fórmulas. En concreto,
dado que si algo que no sea cero se halla incluido bajo tal expresión, el universo
entero se halla también incluido, no será necesario escribir la expresión 
con
la que comienzan todas ellas.
Supongamos que f y g son relativos generals que designan relaciones entre cosas y momentos. En este caso las seis formas de proposición bi-dimensional de Mitchell se presentan de la siguiente forma:
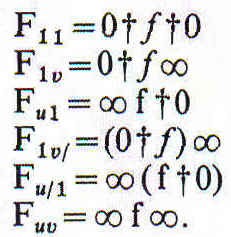
Es evidente que 
pues
Si una de las premisas es entonces 0†f†0 y la otra contiene g, podemos sustituir g por el producto (f, g).
De las dos premisas
por aplicación de las fórmulas
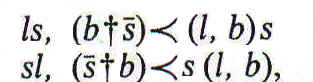
obtenemos
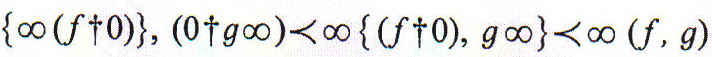
Estas fórmulas nos proporcionan la primera columna de la regla del doctor Mitchell de la página 90.
También son aplicables las siguientes fórmulas:
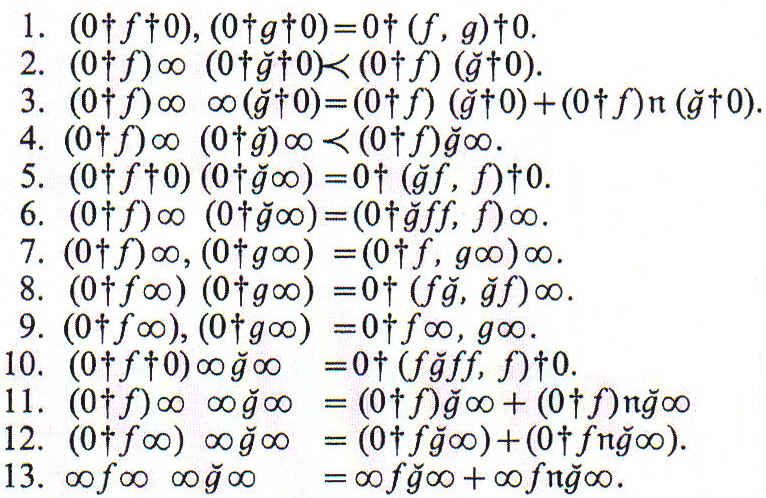
Cuando aparecen a la vez operaciones relativas y no-relativas, las reglas del cálculo se complican considerablemente. En tales casos, lo mismo que en aquellos que involucran relaciones plurales (o que median entre tres o más objetos), generalmente resulta conveniente recurrir a los coeficientes numéricos mencionados antes. Toda proposición, cualquiera que ésta sea, equivale a enunciar que algún complejo de agregados y productos de tales coeficientes numéricos es mayor que cero. Así, por ejemplo,
ΣiΣjlij>0
significa que algo es amante de algo, y
ΠiΣjlij>0
significa que todo es amante de algo. Pero al escribir las desigualdades omitiremos con toda naturalidad la expresión >0 con la que acaban todas. Con lo que las anteriores proposiciones se escribirán
ΣiΣjlij y ∏iΣjlij
Otros ejemplos son los siguientes:
∏iΣj (l)ij (b)ij
significa que todo es a la vez un amante y un benefactor de algo.
∏iΣj (l)ij (b)ji
significa que todo es amante de un benefactor de sí mismo.
ΣiΣk∏j (lij+bjk)
significa que hay algo que está con otro algo en la relación de amar todo salvo los benefactores de él.
Supongamos que a denota el relativo triple "acusador ante — de — —" y ε el relativo triple "defensor ante —de — —". Entonces,
Σi∏jΣk (a) ijk (ε)jki
significa que se puede hallar un individuo, i, tal que, tomando otro individuo cualquiera, j, siempre será posible encontrar un tercero, k, tal que i sea un acusador ante j de k, y j un defensor de i ante k.
Supongamos que π denota "preferidor — de — a —". Entonces
∏iΣjΣk (a)ijk (ejki+πkij)
significa que habiendo tomado un individuo i cualquiera, siempre será posible hallar dos, j y k, tales que i sea un acusador ante j de k y también sea o bien defendido por j ante k o bien algo que k ha preferido a j.
Cuando tenemos algunas de las premisas expresadas de este modo, la conclusión se deduce enseguida mediante la aplicación de las elementales reglas siguientes. En primer lugar, tenemos
En segundo lugar, tenemos las fórmulas
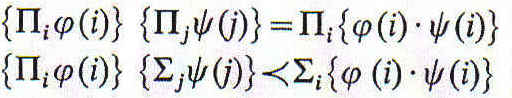
En tercer lugar, como los coeficientes numéricos son todo ellos o cero o la unidad, se les puede aplicar el cálculo booleano.
El siguiente es uno de los ejemplos más simples posibles. Supongamos que se trata de eliminar sirviente de las dos premisas siguientes:
Primera premisa. Hay alguien que acusa a todo el mundo ante todo el mundo, salvo que éste sea amado por alguna persona que es sirviente de todos los no acusados ante él.
Segunda premisa. Existen dos personas, la primera de las cuales defiende a todo el mundo ante todo el mundo, salvo que el no defendido sea beneficiado por la segunda, sin que la persona ante la que no es defendido sea sirviente de ella.
Estas premisas se pueden escribir del siguiente modo:
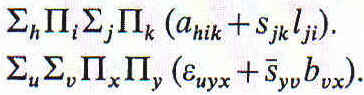
La segunda se puede transformar por inferencia inmediata en
Combinando ésta con la primera tenemos:
Por último, aplicando el cálculo booleano obtenemos la conclusión buscada
La intepretación de ésta es que o bien hay alguien defendido por una persona ante la que él acusa a alguien, o bien alguien defiende a alguien ante su (del defensor) amante, o bien alguien acusa a su propio benefactor.
Generalmente, este procedimiento puede abreviarse mediante el empleo de operaciones intermedias entre ∏ y Σ. Así, por ejemplo, podemos emplear ∏', ∏'', etc., para indicar los productos para todos los individuos menos uno, menos dos, etc. Así,
significará que todas las personas menos una son amantes de todo el mundo menos de sus benefactores, y a lo sumo de dos no-benefactores. De igual modo, Σ', Σ'', etc., denotarán las sumas de todos los productos de dos, de todos los de tres, etc. Así,
significará que hay cuando menos tres cosas en el universo que son amantes de sí mismas. Es evidente que si m<n, tenemos
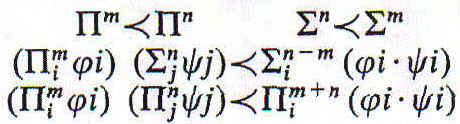
El señor Schlötel ha escrito a la London Mathematical Society acusándome de
haber plagiado sus obras en mi Algebra o Logic. También me ha escrito
a mí para informarme de que ha leído esta Memoria con "heitere Ironie",
así como de que el profesor Drobische, la Academia de Berlín y yo formamos un
"liederliche Kleeblatt", y muchas otras cosas del mismo jaez. Hasta
la fecha de la publicación de mi Memoria, no había visto nunca ninguna de las
obras de Schlötel; después, yo me he procurado su Logik y él se ha
sentido en la obligación de mandarme dos recortes de sus artículos, creyendo,
al parecer, que yo podría sentir curiosidad por ver los pasajes de los que me
había apropiado. Pero habiendo examinado estas producciones, no he encontrado
en ellas ninguna idea que yo haya expuesto nunca, o sea probable que lo vaya
a hacer, como mía propia.
Fin de "La lógica de relativos" (1883). Traducción castellana de Pilar Castrillo. Fuente textual en CP 3.328-358. © de la traducción: Alianza Editorial
Una de las ventajas de los textos en formato electrónico respecto de los textos impresos es que pueden corregirse con gran facilidad mediante la colaboración activa de los lectores que adviertan erratas, errores o simplemente mejores traducciones. En este sentido agradeceríamos que se enviaran todas las sugerencias y correcciones a sbarrena@unav.es
Fecha del documento: 3 de julio 2006
Ultima actualización: 3 de julio 2006