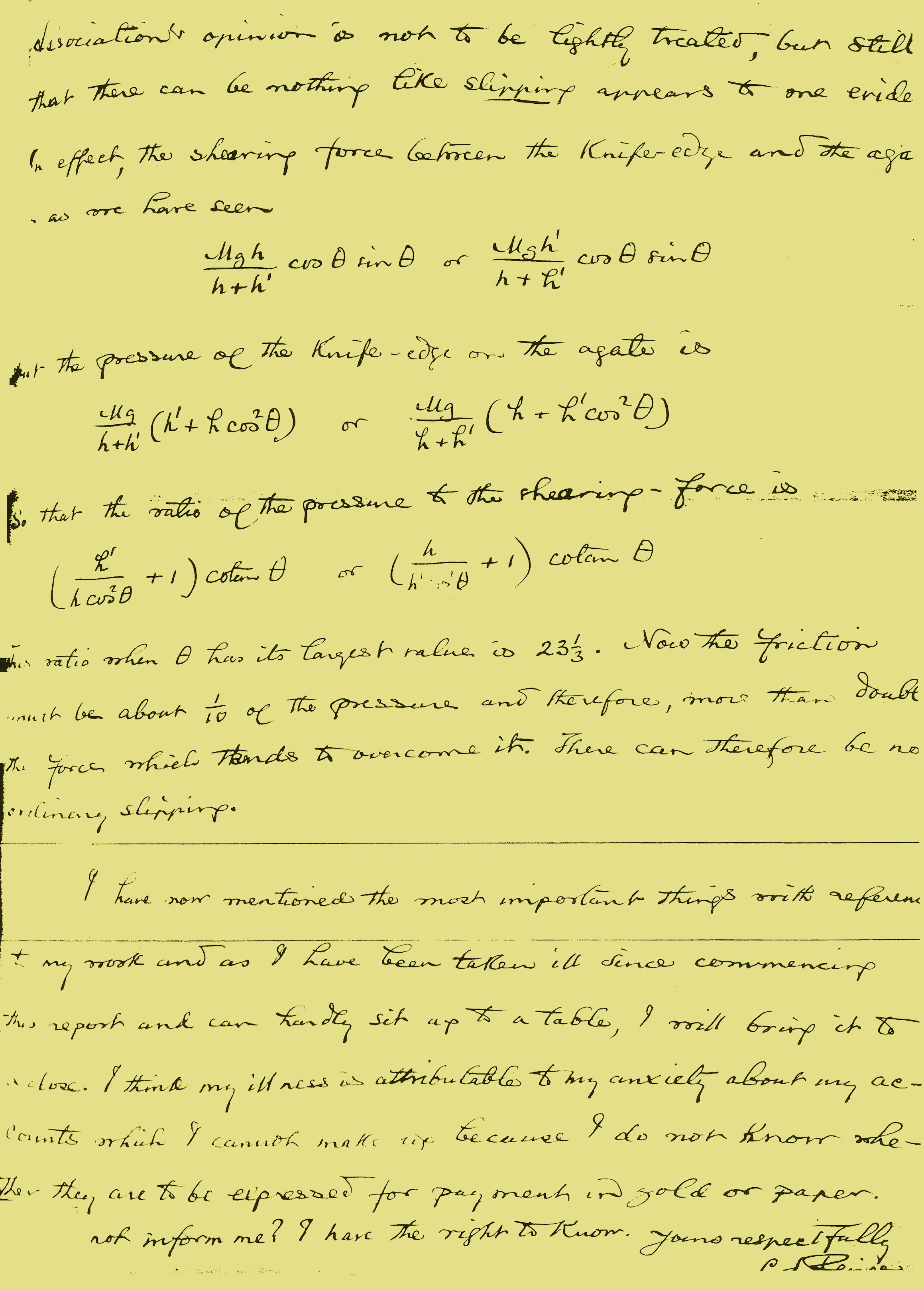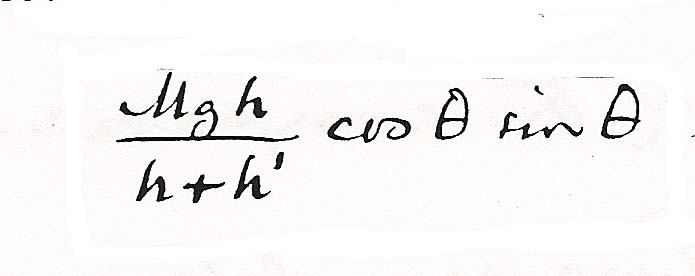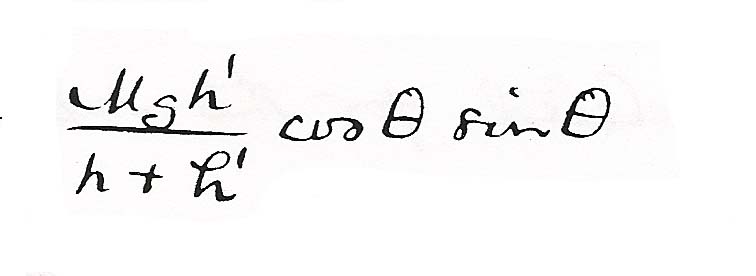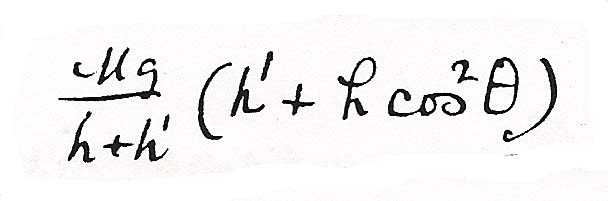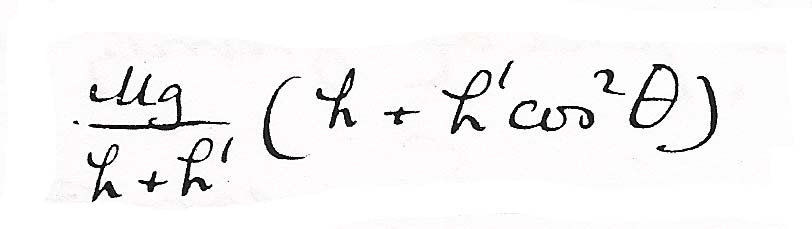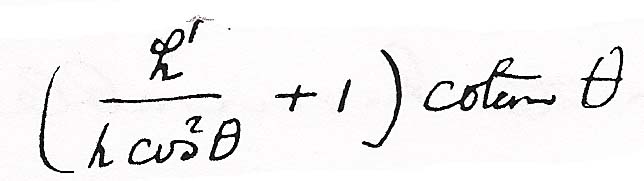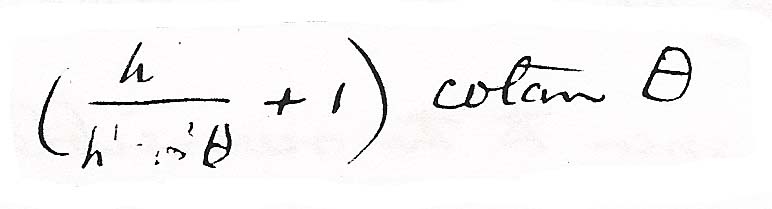Letter from Charles S. Peirce to Carlile P. Patterson
(Paris, 23.09.1875)


 

Spanish translation & annotations
Previous /Next

 

Paris 1875 September 23
Boulevard Haussmann184

Dear Sir

I have now to report upon the progress of my work during the months of August and September. Briefly what I have done is this:

1. I have swung my new pendulum during 16 days at Geneva.

2. I have made important experiments on the flexure of the stand & have investigated the effect of this flexure on my result.

3. I have designed and ordered made in Geneva a vacuum chamber for the reversible pendulum.

4. I have assisted at the seances of the International Geodetical Association & also of the Permanent Commission, where the subject of pendulums has been minutely discussed.

5. I have nearly completed the calculations of the work at Geneva and before the 1st of January shall send you a detailed report upon it.

6. I have continued the calculations of American work but without making much progress as I preferred to push the Geneva calculations.

7. I have devoted considerable time to studying French.

8. I may mention that I have advanced considerably my researches on Stellar Photometry & have commenced the printing.


I will now report a little more fully on these 8 heads and finally will add some miscellaneous information.

I. I think it will be well to say a few words about the history of the reversible pendulum. In the early days of dynamics, the pendulum afforded difficult problems, in the consideration of which two of the most useful general principles of mechanics were discovered. But after the problem of the compound pendulum was once understood it was very easy to deduce the principle of the reversible pendulum. It was Bohnenberger who first proposed to use a reversible pendulum to obtain an absolute measure of the force of gravity. But Bohnenberger’s pendulum (and Kater’s too) was like any pendulum subject to a correction for the resistance of the air. It was Bessel who first proposed to make the pendulum perfectly symmetrical in form and who showed that in this way the whole effect of the air to both dynamical and statical would be eliminated no matter what the law of the resistance of the air might be. (He showed it is true that a very minute effect would remain but one far within the limits of errors of observation.) This is not all that Bessel did. He also proposed when the pendulum had been made approximately reversible to determine the position of the centre of gravity and so correct the time of oscillation and the lenght of the seconds pendulum & he

 

 

 

 
gave perfect formulae for this purpose. When the Swiss Geodetical Commision began their labors in 1862, I think, (I have no books at hand) they heard that Repsold desired to make a reversible pendulum according to Bessel’s design. Bessel had in fact given the proportions of all the parts of such a pendulum. They therefore agreed to order such a pendulum of Repsold. That I learned from Plantamour. But when the pendulum came, it had an adjustment for making it perfectly reversible instead of an apparatus for finding the centre of gravity. Apparently the Swiss men of science never looked at Bessel’s work. (Cellérier told me he had never seen it) and never misdoubted that the pendulum sent was what Bessel designed. Plantamour soon found the instrument utterly impractical and Cellérier then suggested the very method which Bessel had intended. The method is attributed to Cellérier in Plantamour's original & nobody since has given Bessel the proper credit for it, for Dr. Bruhns very wrongly attributes to Bohnenberger the complete theory of the instrument. That is very wrong for the greatest merit of it is its eliminating the effect of the air & that it does so was proved by Bessel. Without the idea of getting the centre of gravity it would have been nearly impractical & that idea is also Bessel’s. But Dr. Bruhns seems not to understand the instrument very well, for in his discussions of the experi

 
ments made in Berlin he says the results are only provisional because not yet corrected for the buoyancy of the atmosphere! But there is no such correction to be made. Cellérier, then discussed the reversible pendulum in a paper which is entirely inferior to Bessel’s but which proceeds according to the same method. The proceedure is however so curtailed as to make the reasoning quite inconclusive to my mind if it is not positively wrong. But the formulae happily contain no important error and are very convenient to use.

Cellérier's formulae embrace the law of the diminution of the arc of vibration upon which Bessel did not touch.

Professor Plantamour's original memoir describing his first experiments at Geneva with the new apparatus naturally laid the foundation of the method of working with the reversible pendulum and must form a model for all later experimenters. Plantamour discarded the method of observing the coincidences of the gravity pendulum with a clock pendulum in order to obtain the rate of oscillation of the former, and for the first time observed transits which were recorded upon a chronograph. The transits which he observed were those of a spot on the pendulum over the thread of a telescope placed at a distance of 5 ½ metres. This method is, in my opinion, the greatest value. M. Plantamour swung his pendulum for equal times with the light end and with the heavy

 

 
   

 
end up, which naturally limited the time of the experiment, because the pendulum will not swing very long with the heavy end up. He avoided arcs greater than 2º or less than ¾º. He made it a rule to have the mean arc of vibration the same in the two positions of the pendulum, so as to avoid any effect of the difference in the resistance of the air with different arcs. His experiments lasted 2500 seconds in each position of the pendulum, or about 42 minutes. With the fine clock of the Geneva observatory, this short interval is perhaps sufficient; although I should prefer a longer one. But in the field, I think very bad indeed to be obliged to depend on the rate of a clock or chronometer for 3/100 of a day. I believe that in that time it may easily have irregularities amounting to √3/100 or say 1/6 of those which it has during a day, that is perhaps to 1/20 of a second or 1/50,000 of the whole time of vibration, which would produce an error of 1/25,000 in the length of the seconds pendulum.

Since Plantamour's pendulum was made, the Repsold's have introduced some changes in the construction of these instruments some of which are real

 

                 

 

 
improvements while some are injuries. They now give the pendulum precisely the length of a metre between the knife-edges, which is an obvious advantage. The form is almost a figure of revolution so that it can be tested in a lathe. The true and hollow weights are more fixed. On the other hand, the pendulum is lighter, so that notwithstanding its greater length the resistance of the air affects its arcs of vibration twice as quickly as with Plantamour's. This is a very great disadvantage. Finally, at Professor Oppolzer’s suggestion, they have made the stand to take to pieces and, in the desire to render it portable and light, they have so grievously affected its rigidity that it may be doubted whether the results obtained with it have much value. Finally Repsold has introduced a metallic thermometer into his standard, most advantageously.

The only experiments made with the new apparatus with which I am acquainted are those of Dr. Albrecht, at Berlin, Leipzig, Mannheim, etc. He at first observed transits like Plantamour but afterwards, injudiciously I think, changed to the method of coincidences and at the same time reduced his time of vibration to 1000 seconds! This is to ignore the irregularities of the motions of the two pendulums entirely. Like Plantamour he swings for equal times with the two ends up.

 

 

 

 


In my experiments at Geneva, I introduced some slight changes in the modes of observing.

1st I place my telescope at one third of Plantamour’s distance, he not having observed that the mean time of the transits when an equal number are taken to the right and left is independent of any eccentricity in the position of the wire.

2nd Instead of taking transits every ¾ second, I never have an interval of less than 2 seconds between successive transits.

3rd It may be supposed that the "physiological time" or interval between the true and recorded passage, differs with the large velocity at the beginning of the experiment from what it is with the small velocity at the end. To make the apparent velocities of the pendulum always nearly the same I employ several different eyepieces of different magnifying powers upon my telescope. At the same time I have specially investigated the effect by experiments with different eyepieces so taken that the mean time of each was the same.

4th The effects of the times of vibration with the two ends up are not the same upon the resulting length of the seconds pendulum. Consequently, the effect of

 

 

 

 

 

 

 

 
errors in the two rates is not the same. Supposing that the errors in the rates obtained are inversely as the time of swinging, which is nearly enough right, I make the times of swinging such that the effect of errors will be nearly the same whichever end is up. Now it is a mechanical proposition that these times will be in the proportion of the times in which the resistance of the air and the friction of the knife-edges will reduce the arc of vibration by any fixed amount. Consequently, I derive the elegant rule that the arc of vibration at the beginning and end should be the same, when the condition that the resistances should have the same effect on the time will be not merely approximately, as in Plantamour's method, but exactly fulfilled. I thus unite two advantages by a mere simplification of the method. But there is a third. For I begin with an arc of 2 1/2º, take other sets of transits at 2º, 1 ½º, 1º, 1/2º, and thus have 4 independent determinations of the length of the pendulum for each set of experiments which 4 determinations relate to 4 different values of

                 

 

 

 the arc.

5th The mercurial thermometer, a normal instrument by Greinert and Geysler (of which I had two but one was injured in transportation by the breaking of the mercury) was read accurately to hundredths of a degree centigrade. It was suspended at the middle of the standard of length and was only relied on to show the manner in which the pendulum changed into length during the time of swinging. The length of the pendulum was compared with the standard immediately before and after each swing and the metallic thermometer was then read and is supposed to show the length of the standard.

I will now make a few remarks in regard to the circumstances under which I made my experiments in Geneva. I mentioned in my last report that Professor Plantamour was absent from Geneva when I arrived there. As soon as he returned, he showed me the greatest kindness and did everything for me that could be imagined. The observatory is not particularly well suited for such experiments as it is very small and there is nothing but the asphalt floor to set the instrument on. When Plantamour made his own experiments he locked up the buil

 

 

                 

 

 
ding and let no one come in. About noon many persons come to the observatory to set their watches. In order to get as favorable circumstances as possible I began my experiments every day at as early an hour as possible but owing to the difficulties of getting breakfast etc. my experiments used to begin at about 6 A.m.

I now pass to the second head of my report. Suspecting that my pendulum staff was not stiff enough, I fixed to the tongue upon which the pendulum rests an engraved scale of tenths of millimetres and before it, upon a stand entirely independent of that of the pendulum, I fixed a microscope provided with a filar micrometer. Then, by means of a very nicely made pulley, I applied a horizontal force to the tongue aforesaid equal to one fourth of the weight of the pendulum when I found that the deflection amounted to 0.10mm, an enormous amount. To find how much this affects the deduced length of the seconds pendulum, I reason as follows. Let the position of the pendulum at any instant make an angle with the vertical equal to . Then, it is evident that its centrifugal force is so very slight compared with its weight that we may negclect it.

 

 

 

 

But in considering the statical Pressure we may regard the mass of the pendulum as concentrated upon the knife edge and upon its centre of oscillation (the other knife-edge) in such a way as to leave the position of the centre of gravity undisturbed. If the distances of the two knife-edges from the centre of gravity are h and h’ and Mg is the weight of the pendulum, the two masses into which we may suppose it divided are

and .

When the pendulum makes an angle with the verticalin the one case

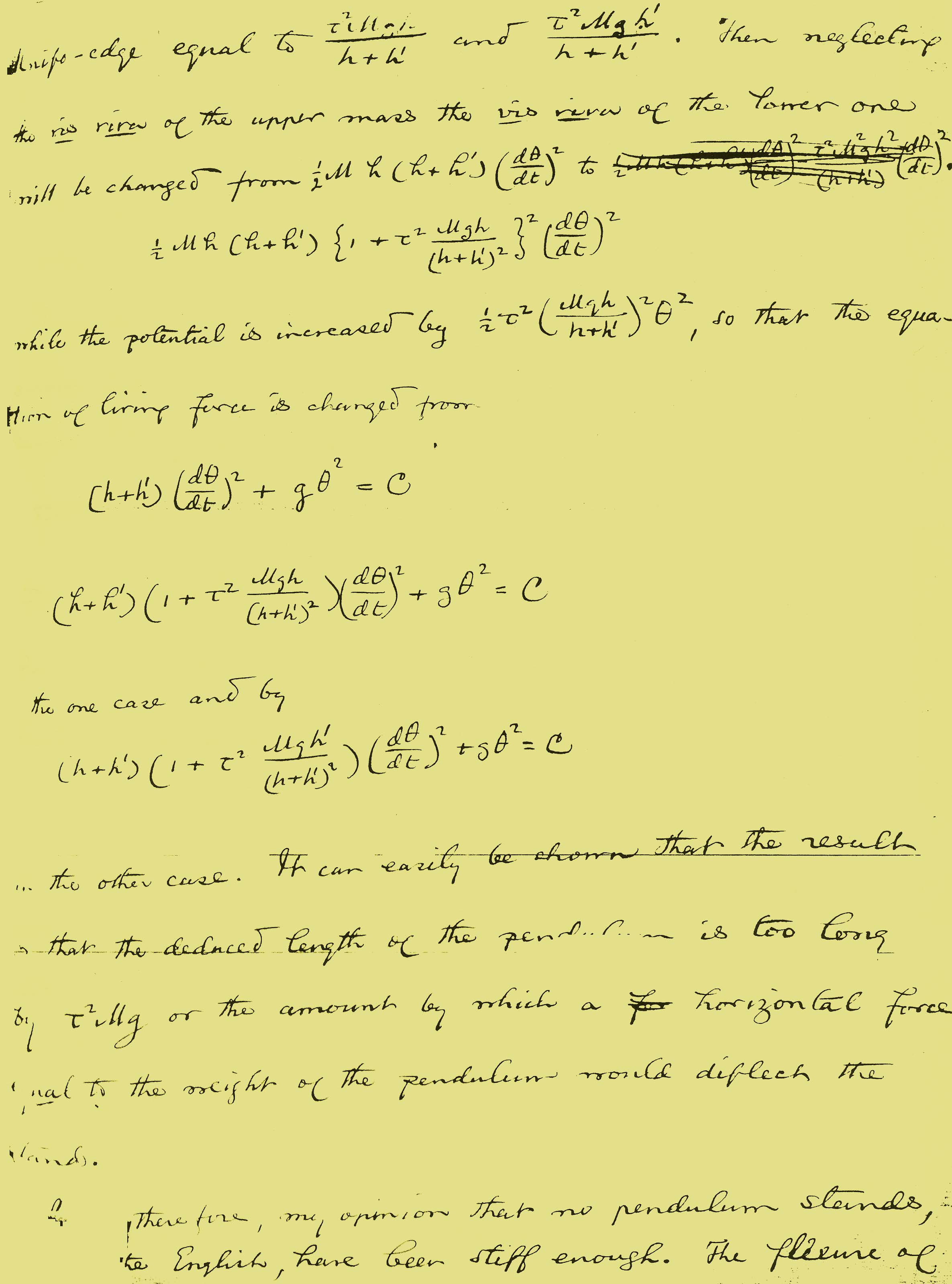
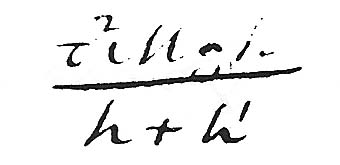and in the other represents the pull of gravity on the pendulum, and

 

and

the force tending to diflect the point of support in a horizontal direction.

The amount of horizontal diflection will be proportional to the force. Suppose the diflection divided by the force to be represented by . Then the horizontal diflection in the two cases is

and

Omitting , which is nearly unity, it follows that the line passing through the two masses when produced cuts the vertical position of the same line produced at a height above the upper

 

 

 

              

 

 

 

 

 

 
knife-edge equal to and 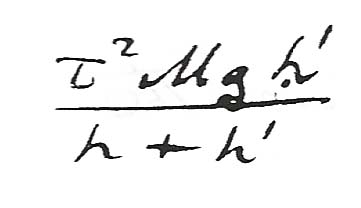. Then neglecting the vis viva of the upper mass the vis viva of the lower one will be changed from to

while the potential is increased by, so that the equation of living force is changed from



to
on the one case and by

in the other case.

It can easily be shown that the result is that the deduced length of the pendulum is too long by [fórmula] or the amount by which a horizontal force equal to the weight of the pendulum would diflect the stand. It is, therefore, my opinion that no pendulum stands, except the English, have been stiff enough. The flexure of

     

 

 

 

 
Bessel's stand has, I am told, been measured by Dr. Peters. I haven’t his paper at hand but undoubtedly Bessel's stand was pretty stiff. The stand of the reversible pendulum of the Prussian Geodetical Institute is undoubtedly considerably stiffer than mine because it was made before they had invented the way of making the thing portable by having it come to pieces but the lenght of the seconds pendulum at Berlin as deduced by experiments with that instrument is 0.18 of a millimeter longer than Bessel got. The difference is undoubtedly due to the greater flexure of the modern stand. Dr. Bruhn's in his reduction of the experiments very hastily attributes the discrepancy to the fact that the value obtained with the reversible pendulum is uncorrected for the buoyancy of the air; whereas, in fact, no such correction has to be applied.

An apparatus to measure accurately the flexure of the stand will in future be regarded as an essential part of all pendulum experiments.

III. When I arrived in Geneva, I found M. Plantamour entirely opposed to my idea of swinging the reversible pendulum in vacuo, but he fully admitted the value of

 

              

 

 

 
the idea before I left. In effect, I expect in that way first to avoid the effect of accidental currents of air; 2nd to make the temperature more steady, 3rd to make it advantageous to use the smaller arcs of vibration, 4th to continue the experiments for a longer time. I wrote to you for authority to construct a vacuum chamber but not receiving any reply of any kind, I have proceeded to do so. I have decided upon a cylinder of copper with glass bells at the bottom and top; the whole to rest upon a collar at the top. There is also to be a system of three iron pillars upon which it may rest. The metallic thermometer will be placed within the chamber. The instrument is being constructed by the Société Genèvoise pour la construction des instruments de physique.

IV. On arriving in Paris, I met Gen. Baeyer who informed me that the session of the International Geodetical Association was being held & the next day I received from the president Gen. Ibañez an invitation to take part in the discussions both of the general conference and of the standing committee, which I did. I gave an account of my work which will be published, and the standing committee presented to the association a resolution very nicely worded, which, without presuming in any way to patronize the Coast Survey, expressed the desire which they had to see my work in Europe happily completed for the sake of the comparison it would afford between the different European determinations of the absolute force of gravity & the connection it would give to the various European pendulum experiments. The resolution was unanimously adopted.

 

 

              

 

 

The subject of the pendulum was minutely discussed. The preference was given to the reversible over the invariable pendulum, quite rightly I do not doubt. It was at the same time admitted that there were various defects in the apparatus. These were not precisely specified in the resolution adopted except that it was recognized as desirable to ascertain whether the axis of rotation of the pendulum coincided with the knife-edge. This referred to a matter broached by Oppolzer, who thinks that as the pendulum swings there is a motion of the knife-edge upon the agate. He even pretends to have demonstrated this by means of an instrument devised for the purpose. I confess I am skeptical about it. I will have one of his instruments since the Geodetical

 

 

 

 

 

 

              

 

 
Association's opinion is not to be lightly treated, but still that there can be nothing like slipping appears to me evident. In effect the shearing force between the knife-edge and the agate is as we have seen

or

but the pressure of the knife-edge on the agate is

or


So that the ratio of the pressure to the shearing-force is

or

This ratio when has its largest value is 23 1/3. Now the friction must be about 1/10 of the pressure and therefore, more than double the force which tends to overcome it. There can therefore be no ordinary slipping.

I have now mentioned the most important things with reference to my work and as I have been taken ill since commencing this report and can hardly sit up to a table, I will bring it to a close. I think my illness is attributable to my anxiety about my accounts which I cannot make up because I do not know whether they are to be expressed for payment in gold or paper. Will you not inform me? I have the right to know.


            Yours respectfully.


C. S. Peirce


Traducción de Sara Barrena (2013)
Una de las ventajas de los textos en formato electrónico respecto de los textos impresos es que pueden corregirse con gran facilidad mediante la colaboración activa de los lectores que adviertan erratas, errores o simplemente mejores transcripciones. En este sentido agradeceríamos que se enviaran todas las sugerencias y correcciones a sbarrena@unav.es
Proyecto de investigación "Charles S. Peirce en Europa (1875-76): comunidad científica y correspondencia" (MCI: FFI2011-24340)

Fecha del documento: 12 de marzo 2013
Última actualización: 25 de mayo 2022
[Página Principal]